Cylindrical Coordinate System:-Cylindrical co-ordinate system is a three dimensional co-ordinate system that specifies point positions by the distance from a chosen reference axis,the direction from the axis relative to a chosen reference direction & the distance from a chosen reference plane perpendicular to the axis.The latter distance is given as a positive or negative no depending on which side of reference plane faces the point.
HSL & HSV are the two most common cylindrical co-ordinate system.HSL & HSV are developed in 1970.They are widely used today in color pickers in image editing software,less commonly in image analysis
& computer vision.
HSV:-HSV stands for Hue,saturation & value.often also called HSB ,B for brightness. It is also called hex cone model.
HSL:- HSL stands for hue,saturation & light ,often also callled HLS.It is also called double hex cone model.
*We can calculate Chroma from RGB with the following formula :-
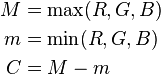
*We can calculate Hue from RGB with the following formula :-

*We can calculate Lightness from following formula :-
(i)In the HSI model intensity is defined as average of three components:
I = 1/3(R+G+B)
(ii)In the HSV "hexcone" model value is defined as the largest component of color.
V=M=max(R,G,B)
(iii)In the bi-hexcone model lightness is defined as the average of largest & smallest color component.
L= 1/2(M+m)
(iv)Luma is the weighted average of gamma corrected R,G & B

* Following are the formula for the saturation for HSV,HSL & HSI:-
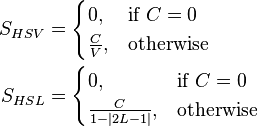

Uses of HSI,HSV & HSL:-HSI ,HSV & HSL are often used computer vision,Image analysis for feature detection & image segmentation.It is used in robot vision ,object recognition,content based image analysis & analysis of medical images.It is also used in color pickers of image editors.
HSL to RGB:-
For converting HSL to RGB ,First of all ,we need to compute chroma:-

where C is Chroma
L for Lightness
Shsl for saturation
Next,we find the point on one of the bottom three faces of the RGB cube which has the same hue & chroma as our color.


Finally ,we add the equal amounts of R,G & B to reach the proper value.
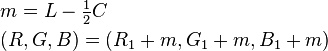
HSV to RGB:-
For converting HSV to RGB ,First of all ,we need to compute chroma,by multiplying saturation by the maximum chroma for a given value.

where C is Chroma
V for value
Shsv for saturation
Next,we find the point on one of the bottom three faces of the RGB cube which has the same hue & chroma as our color.


Finally ,we add the equal amounts of R,G & B to reach the proper value.

Luma/Chroma/Hue to RGB:-


Finally ,we add the equal amounts of R,G & B to reach the proper value.

HSL & HSV are the two most common cylindrical co-ordinate system.HSL & HSV are developed in 1970.They are widely used today in color pickers in image editing software,less commonly in image analysis
& computer vision.
HSV:-HSV stands for Hue,saturation & value.often also called HSB ,B for brightness. It is also called hex cone model.
HSL:- HSL stands for hue,saturation & light ,often also callled HLS.It is also called double hex cone model.
*We can calculate Chroma from RGB with the following formula :-
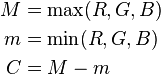
*We can calculate Hue from RGB with the following formula :-

*We can calculate Lightness from following formula :-
(i)In the HSI model intensity is defined as average of three components:
I = 1/3(R+G+B)
(ii)In the HSV "hexcone" model value is defined as the largest component of color.
V=M=max(R,G,B)
(iii)In the bi-hexcone model lightness is defined as the average of largest & smallest color component.
L= 1/2(M+m)
(iv)Luma is the weighted average of gamma corrected R,G & B

* Following are the formula for the saturation for HSV,HSL & HSI:-
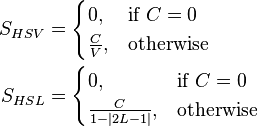

Uses of HSI,HSV & HSL:-HSI ,HSV & HSL are often used computer vision,Image analysis for feature detection & image segmentation.It is used in robot vision ,object recognition,content based image analysis & analysis of medical images.It is also used in color pickers of image editors.
HSL to RGB:-
For converting HSL to RGB ,First of all ,we need to compute chroma:-

where C is Chroma
L for Lightness
Shsl for saturation
Next,we find the point on one of the bottom three faces of the RGB cube which has the same hue & chroma as our color.


Finally ,we add the equal amounts of R,G & B to reach the proper value.
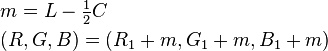
HSV to RGB:-
For converting HSV to RGB ,First of all ,we need to compute chroma,by multiplying saturation by the maximum chroma for a given value.

where C is Chroma
V for value
Shsv for saturation
Next,we find the point on one of the bottom three faces of the RGB cube which has the same hue & chroma as our color.


Finally ,we add the equal amounts of R,G & B to reach the proper value.

Luma/Chroma/Hue to RGB:-
Here we already have Hue & Chroma so we use same strategy:-


Finally ,we add the equal amounts of R,G & B to reach the proper value.

No comments:
Post a Comment